集合基数统计
集合基数:对于非无限集合,基数是指集合中元素的个数。
合并:将两个集合合并后,如何求新集合的基数。
Bitmap –> Linear Count –> LogLog Count –> Adaptive Count –> HyperLogLog Count
假设集合的基数为 n
Bitmap
原理:每一位 bit 代表一个集合中的元素,举例:00101011 可以代表自然数的集合(3, 5, 7, 8),通过数 bitmap 中 1 的个数可以得知集合的基数。
合并:将代表两个集合的 bitmap 按 bit 或(or)得到新的 bitmap 即可代表新的集合
内存占用:需要 n bit,空间复杂度 O(n)
Linear Count
原理:已知哈希函数的结果空间为 1~m,则申请一个 m 位的 bitmap,并将每一位的初始值设置为 0。对集合中的每个元素作哈希得到值为 k,则将 bitmap 中第 k 位置为 1。
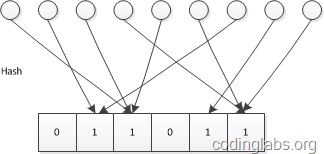
经过公式推导可以得到基数 n 和 值为 0 的 bit 个数 u 以及总位数 m 的关系: $n=-mlog \frac um$
合并:和 bitmap 相同
内存占用:由于当桶满的情况(即所有 bit 都为 1)下,u=0,公式得到的值趋近无穷,不再生效,因此需要控制满桶出现的概率足够小,并且需要控制误差在可接受范围内,经过一系列计算,可以得出 m 和 n 的一个表格,表示不同集合基数 n 时,需要控制满桶概率的 m 的值,可以总结出一个规律,m 大约为 n/10,即只需要 bitmap 方式占用空间的十分之一。但是从渐进复杂性的角度看,空间复杂度仍为 O(n)
误差:由 n 的量级和 m 的量级共同决定,当可以容忍的误差为 ∆ 则可以推导得到 $m > \frac {e^t-t-1}{(∆t)^2}$ 其中 t = n/m
LogLog Count
前置要求:
- 哈希的结果分布近似均匀
- 哈希结果碰撞的概率足够小
- 哈希的结果表示为二进制后长度固定
原理:
将集合中一个元素进行哈希后,表示为 m 位二进制存入 bitmap,存入时与原 bitmap 中的值做 或(or) 操作,由前置要求的第 x 条可知,每一 bit 为 0 或为 1 是互相独立的,各有 1/2 的概率,因此将集合中所有元素全部存入 bitmap 的过程可以看作是 伯努利过程,那么第 k 位第一次出现 1 的概率为 $P_n(x=k) = \frac {1}{2^k}$。接下来用反证法证明,集合的基数 $n ≈ 2^k$
- bitmap 中 1 第一次出现在 k 位之前的概率 $P_n(x≤k) = (1-P_n(x=k))^n = (1 - \frac {1}{2^k})^n$
- 那么 bitmap 中 1 第一次出现在 k 之后的概率 $P_n(x>k) = (1 - P_n(x≤k)) = (1 - (1 - \frac {1}{2^k})^n)$
首先,假设 $n » 2^k$ 那么 $P_n(x>k)$ 趋近于 0,而当 $n « 2^k$ 时,$P_n(x≤k)$ 则趋近于 0,于是 n 可以近似由 $2^k$ 求得。
此时已经可以得到集合的基数为 $$n ≈ 2^k$$ 其中 k 为 bitmap 中从高位数起,1 第一次出现的位数。
桶平均
接下来,为了抵消一些偶然因素,LLC 引入了桶分组,类似于物理实验中的多次实验求平均值。
将元素哈希后的 m 位二进制表示,拆分为两部分,前 p 位表示桶序号,后面的 m-p 位作为真正用于估计基数的比特串。桶序号相同的元素被分配到同一个桶,估计基数时,首先计算桶内比特串 1 第一次出现的位置,记为 P[i],然后对 p 个桶加和取平均后再进行估算,此时 n 的估计值变为 $$n ≈ 2^{\frac {∑P[i]}{p}}$$
合并:以桶为合并的最小单位,桶序号相同的比特串进行 bitmap 的合并 内存占用:内存使用与分桶数及哈希后的二进制位长度相关,假设哈希后数值表示为二进制为 32 位,则每个桶需要 5bit 内存来存当前桶第一个 1 出现的位置,内存占用即为 $$\frac {5*p}8 byte$$ 误差:误差主要由分桶的数目决定,如果要将误差控制在 ∆ 之内,则分桶数 p 的取值为 $$p > (\frac {1.30}{∆})^2$$
假设基数为一亿的集合(约为 $2^27$),分桶数为 p=1024,那么需要占用的内存为 5*1024/8=640 字节,误差由 $1024 > (\frac {1.30}∆)^2$ 可算得 $∆ < 0.040625$ 即小于 4%
Adaptive Count
基数比较小时,用 LC,比较大时用 LLC
HyperLogLog Count
注意,这里的分桶数,使用 m 来表示,而不是 p
将 LLC 中桶分组的几何平均替换为调和平均,使用调和平均数代替几何平均数后,估计公式变为如下
$$\hat{n}=\frac{\alpha_m m^2}{\sum{2^{-M}}}$$
其中
$$\alpha_m=(m\int _0^\infty (log_2(\frac{2+u}{1+u}))^m du)^{-1}$$ 替换求平均方式的原因是,几何平均对离群值非常敏感,导致有空桶出现时,估计结果有较大扰动
参考:
[1]. 解读Cardinality Estimation算法(第二部分:Linear Counting)
[2]. 解读Cardinality Estimation算法(第三部分:LogLog Counting)
[3]. 解读Cardinality Estimation算法(第四部分:HyperLogLog Counting及Adaptive Counting)
[4]. HyperLogLog
[5]. Hyperloglog 算法简介